数学中的宇宙本质超越无限，解析延拓及其在量子物理中的应用

这是关于复函数的第二部门。你可以在这里找到第一部门

复函数的标致天下，摸索更高维度的暗藏布局。

在第一部门中，我们先容了全纯函数和亚纯函数以及它们的性子。在这一部门中，我们将继续沿着这条路走下去，然则将重点放在另一个关于全纯函数的惊人事实上。

在陈说这些有名的成果之前，让我们先感触感染一下函数的分歧表现方式。

让我们界说函数g如下所示：

很显著|z| < 1，不然级数发散，酿成无限。假如我们把g看作一个复变量的复函数，它的界说域为单元圆盘，即在复平面上以0为中心，半径为1的圆盘。这叫做幂级数的收敛半径。

这都没问题，然则我们可以在这个圆盘上用另一种方式表现这个函数，也便是：

在单元圆盘上这两个函数等同是很容易证实的。但很显著，它们作为函数是不相等的，由于它们的界说域分歧。然而，我们很快就会看到，在某种意义上，这两个函数仅仅是统一函数的两种表现。

我们稍后会回到这个话题。最好先记住这个例子。

第一步是关于全纯函数的一个惊人的事实。

恒等定理

全纯函数的恒等定理表述如下：

给定域D上的两个全纯函数f和g，假如f = g在某个 A ⊆ D 上，此中A有一个，则f = g在D上。这意味着一个全纯函数完全由它在D中的单个开邻域上的值决议。

积点

降维说便是，假如两个全纯函数在一个圆上相等（无论何等小），那么它们在任何处所都相等。

是以某种水平上，为了使函数成为全纯函数而必需经由过程的严厉要求将这种布局置于函数上，以使其所有信息都包括在可想象的最小区域的图像中。局部信息照样全纯函数的全局信息。

解析延拓

假设f是界说在复平面ℂ的非空开子集U上的全纯函数。假如V是ℂ中包括U的较年夜开子集，且F是界说在V上的一个全纯函数，使：

F(z)= F(z)对付U中的所有z，那么F被称为f的解析延拓。

让我们再一次用更容易懂得的词来翻译：

假如两个全纯函数f和F在某个域U上相等，而F在包括U的更年夜的域上是全纯的，则F称为f的解析延拓。

如今，症结是：

恒等定理暗示解析延拓是独一的，假如V上有另一个全纯函数G，使得G(z)=f(z)对付U中的所有z，那么F =G。

这是一个明显的成果。这意味着只有一种办法可以扩大解析函数（假如扩大也必要是解析的）。

假如我们斟酌上面的例子，g是上面的几何级数，g*是即是g在单元圆盘上的关闭情势的表达式，我们如今可以自大地说g*是g在ℂ\{1}域上的独一的全纯扩大。

数学家们倾向于以为解析延拓与它所扩大的函数是雷同的，只是在较小的域上有分歧的可能表现。

解析延拓的利用

这些都没问题，但我们能用它做什么呢。我想最好的例子之一，便是黎曼ζ函数上的功。

我们从界说函数开端：

注意，s的实部必需年夜于1，不然，级数会发散。

函数的经典级数表现的收敛规模

这个函数在统一个域中有另一个表达式，它是所有质数的乘积，叫做欧拉积。

这是巨大的莱昂哈德-欧拉的一个惊人的数学发现，它在函数中暗藏了一些关于质数的信息。

函数的两个表达式相等这一事实，在加法和乘法的天下之间，意味着存在着某种桥梁。事实证实，它们之间真正的桥梁超越了域Re(s) > 1，是以我们必要解析延拓。

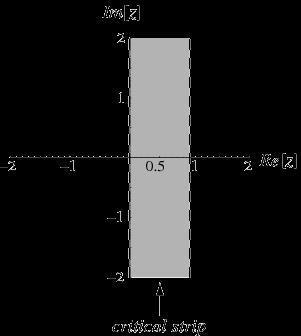
为了提取质数散布的信息，我们从黎曼ζ函数中所必要的信息便是它的零点子集是若何散布的。这个子集是零的聚拢，它位于所谓的临界区间0 <Re(s)< 1上.

注意函数f的0点是一个使f(r) = 0的数r。

黎曼料想所有这些0点都对称地散布于垂直线Re(s) = 1/2上的条形上。这被称为“黎曼假说”，是数学中最年夜的未解之谜之一。

回到主题上来。信息位于收敛区域之外。如今，我们若何继续解析黎曼 ζ函数。

现实上，有几种办法可以做到这一点。我将给你们两种异常有趣的方式。

第一种办法是，假如我们取由上面的无限级数界说的函数，然后减去两个“偶数”项，然后我们获得瓜代的函数：

化简这个等式可以获得：

而且因为可以证实函数对付Re(s) > 0收敛，这现实上是黎曼函数的解析延拓。

另一个神奇的办法是经由过程黎曼本身起首发现的一个函数方程来继续阐发这个函数。

在我看来，这是数学中最美好的关系之一。右边倒数第二个因子叫做γ函数，它是复数阶乘的推广。

我们清晰地看到 ζ函数在负偶数处必需是0，由于sin项在这里消散了。

这给出了除s=1外的整个复平面的解析延拓。该函数方程可作为所有的ℂ上的亚纯函数方程。

评估无穷数目

这个话题在数学界引起了不小的惊动，由于一些物理学门风称，人们可以简单地做一些不合理的操作，好比设置无穷发散级数：

1 + 2 + 3 + 4 +…=-1/12。

这当然是乱说八道（他们也知道这一点）。话虽如斯，在这个偏向上有一些令人不寒而栗的工作正在产生，我以为我们还没有完全懂得。物理学家称它为ζ正规化等一些独特的名字，然则还有一些问题我们还没有解释清晰。

让我试着经由过程一个例子来具体阐明。

事实证实，假如你试图制作一个真空，那么无论你做得有多好，粒子（被称为虚拟粒子）老是会在这个处所呈现或消散。我们如今是在量子力学的范畴，以是当心你的物品不知去向。

这种虚粒子征象被称为量子涨落，这统统都与场有关。不是数学范畴，而是量子范畴。场是空间的一种属性，每个点都有一个值。例如，假如我们以为温度是持续的，那么它就像一个场，由于每个点都有一个值（也便是它的温度）。但我们都知道，由于温度与粒子的动能有关，以是它不是完全持续的。然而，在物理学中，我们研讨的是场，如电磁场或引力场，它们都是真正的场。

上面提到的场是力场，但现实上，物资粒子也有与之相关的场。电子有电子场，上夸克有上夸克场，等等。这是由于所有的粒子（在这个理论中）都是它们地点的场中的引发，例如，光子是电磁场中的一个引发。

这个理论被称为量子场论，它从数学的角度来看异常有趣，由于它涉及到微扰理论、路径积分、对称群和算子。

所有的场，分外是电磁场，都有颠簸。换句话说，在任何给准时刻，它们的现实值环抱一个恒定的均匀值变化。纵然是绝对零度的完善真空也有颠簸场，称为“真空颠簸”。

假如我们把粒子困在两块不带电的导电金属板之间，那么当我们把空间朋分成一份一份时，我们就限定了呈现在两块金属板之间的粒子。成果，会在板块上发射出一个力，由于板块之间的总能量比它们外部的要低，为了计算由这些能量发生的总力，我们获得了一个表达式，此中的一个因素是无穷发散级数：

这看起来像是有人试图用无限级数的界说来计算“ζ（-3）”，而无限级数的界说只容许Re(s) > 1，还记得吗。

这是从哪里来的。看来他们的计算在评估时失足了。从高条理的角度来看，当两个金属板异常靠近（几纳米）时，会产生什么呢。可能在两板之间呈现或消散的虚粒子的数目受到它们的波长的限定，由于它不克不及跨越两板之间的间隔。然而，在外部，粒子没有这种限定，更多的可能性产生了。这就从空间的纯量子力学特征中发生了一种力，将它们推向彼此。

这种征象被称为卡西米尔效应。

在理论计算发生引力的能量时，我们终极不得不将所有可能的驻波或模态能量（也可所以粒子的能量）相加。因为所有驻波的波长都可以写成雷同常数的倍数，是以依据尺寸的分歧，我们会获得与上述类型雷同的发散级数。

在这些计算中，这种能量彷佛是无穷的，但当然，物理学家知道事实并非如斯。假如你看一下上面的级数你必需给它一个有限的值，那么一个很好的预测是解析延拓的黎曼 ζ函数在-3处的值。

究竟，假如你把-3代入黎曼 ζ函数的级数界说中，那么你就获得了我们必要“求值”的无限级数。

让我们用泛函方程来求ζ（-3）。我们必要计算如下：

欧拉奉告我们ζ(4) = π /90当然，1/2³= 1/8Γ(4)= 3 != 6sin（3π/ 2）= 1

当我们把上面的式子代入公式，我们获得：

ζ(-3) = 6 ⋅ π⁴/ 8⋅90⋅ π⁴ = 1 /120。

注意。这不是上述级数的值。这是黎曼ζ函数在点-3处的值。

但令人惊异的是，当物理学家在他们的公式顶用1/120取代无穷时，当他们在试验室里做试验时，它们丈量相识析延拓法所猜测的力的准确量。

这是怎么回事。年夜天然是否吞下了无限无尽的能量。波和能量可以泯没，当所有的虚能量都被抵消了，那么真正的正规化值仍旧存在

但有趣的是，天然彷佛真的批准我们从解析延拓中获得的值。由于毫无疑问，这是一种天然征象，一种源于粒子和场的真实本色的空间量子特征。